Charts and Metric Tensor
Mar 16, 2010
Although the title of this article reads "Charts and Metric Tensor", I will not describe any of these two concepts. I will assume that the reader knows what a chart is and the basic definition of metric tensor (and of course a tensor). In this article I will primarily discuss the relationships between a manifold, the charts laid down on it, and the properties of metric tensor. We will thus try to identify some of the intrinsic properties of a manifold and how charts and metric tensors can explore those.
However just for the reference of the readers the following brief recapitulations may help:
- A manifold is an abstract topological space that is locally Euclidean. Thus a 2-sphere and a torus are 2-dimensional manifolds. If two manifold have the same global topology (i.e. homeomorphic), they are the same manifolds.
- A chart (or coordinate chart),
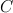, is a parametrization of a manifold, 
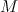. More technically, for a 
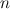-dimensional manifold 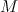, it is an injection from 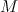to 
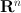. Thus, the system of latitudes & longitudes on a 2-sphere is a chart defined on the manifold of 2-sphere. An atlas is a more generalized notion. But for our discussion charts will be good enough.
- A tensor (or more specifically a tensor field) is an abstract entity that can be associated with a 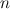-dimensional manifold such that for a given chart, an order-
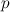tensor field can be represented by 
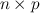real numbers (called the coordinate representation or the components of the tensor in chart 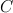). Tensors follow a specific transformation rule - that is, for the same manifold 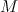, given two charts 
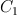and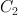 
, the components of the same tensor in the two different charts are related in a specific way. This is the key identifiable characteristic of a tensor.
- A metric tensor introduces the notion of distance on a manifold. By the very property of tensors, we note that for a given manifold 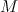, if the components of a metric tensor is stated in a particles chart
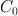, its components get automatically determined in all other charts.
Now we briefly discuss a few immediate observations:
Charts are just constructions - they tell nothing about the local properties of the manifold: That's an easily understandable fact. Charts are just constructions made on a manifold by the mathematician. They are parametrization of the manifold - that is a set of real numbers associated with each point on the manifold so as to identify the point uniquely. Thus they really do not tell anything very informative about the manifold itself. Thus, a chart does not give any notion of distance, scale, etc. If two or more charts are constructed for the same manifold, the relationship between those can be established (the transformations), but still none reflect any intrinsic property of the manifold.
A metric tensor is also a construction, but less arbitrary than charts: Given the coordinate representation in a particular chart, the coordinate representation of the tensor in all other charts get determined by the transformations between the charts. The intuitive way of thinking about this is to consider the coordinate representations of the tensors in different charts as unknown quantities, but are related to each other. Thus if you specify the value in one chart, by the virtue of the relationship between the charts it gets determined in all other charts.
TODO: Finish this